Range within the Electromagnetic Spectrum
Infrared radiation is that part of the electromagnetic spectrum that is immediately adjacent to the red light of approx. 760 nm on the long-wave side of the visible spectrum and extends to a wavelength of approx. 1 mm.
In this respect, the wavelength range of up to approx. 20 µm is of importance to technical temperature measuring.
In the second half of the 19th century, it became known that heat radiation and other electromagnetic waves, such as visible light or radio waves, were similar in nature. This was followed by the discovery of the laws of radiation by KIRCHHOFF, STEFAN, BOLTZMANN, WIEN and PLANCK. By the mid-20th century, intensive and successful work on the military use of infrared technology facilitated the building of first infrared viewers. With some distance in time and technology, also the first thermographic devices for non-military application available in the 60s. Parallel to this, however, in considerably larger diversification of available devices, pyrometry developed to become a wide-spread approach in industrial temperature measuring.
Radiation Laws of the Black Body
The bodies occurring in real life show very diverse radiation properties. Therefore, it has proved worthwhile to initially consider the simplified laws of a model body of ideal radiation properties to be then applied to actually occurring objects. This model body is known in radiation physics as the “black body”. It distinguishes itself by the fact that, of all bodies of equal temperature, it shows the largest possible emitted radiation.
The spectral spread of radiation emitted by a black body is described by PLANCK’s radiation law:
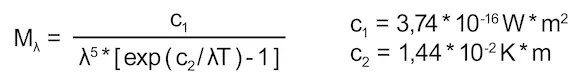
This representation shows that the spectral composition varies with the object temperature. Bodies of a temperature of beyond 500 °C, for example, also emit radiation in the visible range. Furthermore, it must be noted that, at each wavelength, radiation intensity increases with rising temperature.
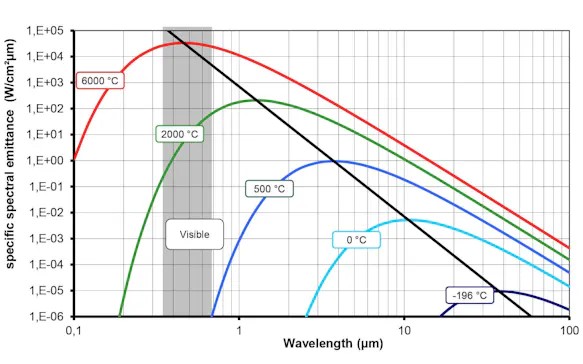
PLANCK’s radiation law represents the principal correlation regarding non-contact temperature measuring. Due to its abstract nature, however, it is not directly applicable in this form to many practical calculations. But a variety of further correlations can be derived from it, two of which shall briefly be mentioned in the following. So by means of integrating, for example, the spectral radiation intensity across all wavelengths, the value of the entire radiation emitted by the body is obtained. This correlation is called the STEFAN BOLTZMANN’s law.
![]()
Due to its simple mathematical correlation, it is well suited for rough estimates, particularly when calculating the heat balance of objects as well as interrelations of total radiation pyrometers. However, the spectral measuring range of most measuring devices is usually strongly limited and, therefore, this equation is inapplicable to this purpose.
The graphic representation of PLANCK’s radiation law shows that the wavelength, at which radiation emitted by a black body has a maximum, shifts with changing temperature. WIEN’s displacement law can be derived from PLANCK’s equation by differentiation.
The lower the temperature of the object to be measured the further its radiation maximum shifts towards larger wavelengths. It is at about 10 µm when close to room temperature.
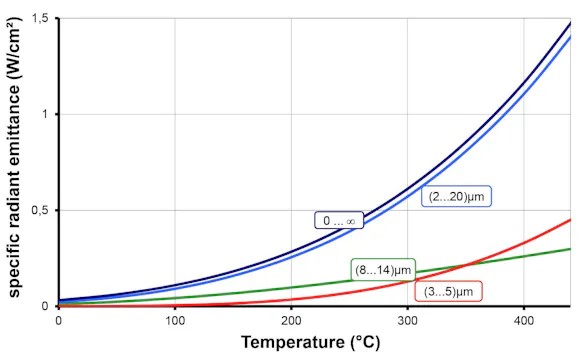
The level of transmittance of air is strongly dependent on wavelength. Ranges of high attenuation alternate with ranges of high transmittance (shaded), the so-called "atmospheric windows". While transmittance in the range of (8 ... 14) µm, i.e., the long-wave atmospheric window, maintains to be equally high over longer distances, measurable attenuation caused by the atmosphere already occurs in the range of (3 ... 5) µm, i.e., the short-wave atmospheric window, at measuring distances of some ten meters.
Influence by the Measured Object
The black body as a radiometric model is indispensable when considering principal correlations. Since real objects that are to be measured deviate more or less strongly from that model, it may become necessary to take this influence into account in measurements. Especially suited for this purpose is the parameter of emittance which is the measure for a body’s capability of emitting infrared radiation. Having a value of 1, the black body has the highest possible emittance, which is additionally dependent on wavelength.
Contrary to this, the emittance of real objects to be measured may show more or less strong dependence on wavelength. The following parameters may also be of some influence:
-
Material composition
-
Oxide film on the surface
-
Surface roughness
-
Angle to the surface normal
-
Temperature
-
Polarisation degree
A multitude of non-metallic materials – at least within the long-wave spectral range – shows high and relatively constant emittance, regardless of its surface structure. These include the human skin in the same as way as most mineral building materials and coating paints.
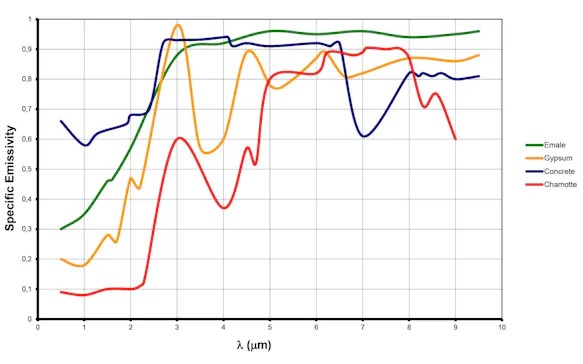
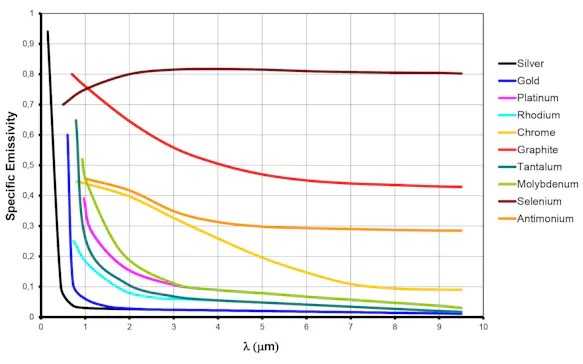
In contrast, metals generally have low emissivity that greatly depends on the surface properties and drops as wavelengths increase.

 English
English Ελληνικά
Ελληνικά



 Login
Login New member
New member